Time value of money
A time value of money calculation is a calculation that solves for one of several variables in a financial problem.
In a typical case, the variables might be: a balance (the real or nominal value of a debt or a financial asset in terms of monetary units), a periodic rate of interest, the number of periods, and a series of cash flows. (In the case of a debt, cash flows are payments against principal and interest; in the case of a financial asset, these are contributions to or withdrawals from the balance.) More generally, the cash flows may not be periodic but may be specified individually. Any of the variables may be the independent variable (the sought-for answer) in a given problem.
Some standard calculations based on the time value of money are:
- Present value: The current worth of a future sum of money or stream of cash flows, given a specified rate of return. Future cash flows are "discounted" at the discount rate; the higher the discount rate, the lower the present value of the future cash flows. Determining the appropriate discount rate is the key to valuing future cash flows properly, whether they be earnings or obligations.[2]
- Present value of an annuity: An annuity is a series of equal payments or receipts that occur at evenly spaced intervals. Leases and rental payments are examples. The payments or receipts occur at the end of each period for an ordinary annuity while they occur at the beginning of each period for an annuity due.[3]
- Present value of a perpetuity is an infinite and constant stream of identical cash flows.[4]
- Future value: The value of an asset or cash at a specified date in the future, based on the value of that asset in the present.[5]
- Future value of an annuity (FVA): The future value of a stream of payments (annuity), assuming the payments are invested at a given rate of interest.
Formula
The following formula use these common variables:
- PV is the value at time=0 (present value)
- FV is the value at time=n (future value)
- A is the value of the individual payments in each compounding period
- n is the number of periods (not necessarily an integer)
- i is the interest rate at which the amount compounds each period
- g is the growing rate of payments over each time period
Future value of a present sum
The future value (FV) formula is similar and uses the same variables.
Present value of a future sum
The present value formula is the core formula for the time value of money; each of the other formulae is derived from this formula. For example, the annuity formula is the sum of a series of present value calculations.
The present value (PV) formula has four variables, each of which can be solved for:
The cumulative present value of future cash flows can be calculated by summing the contributions of FVt, the value of cash flow at time t
Note that this series can be summed for a given value of n, or when n is ∞.[7] This is a very general formula, which leads to several important special cases given below.
Present value of an annuity for n payment periods
In this case the cash flow values remain the same throughout the n periods. The present value of an annuity (PVA) formula has four variables, each of which can be solved for:
To get the PV of an annuity due, multiply the above equation by (1 + i).
Present value of a growing annuity
In this case each cash flow grows by a factor of (1+g). Similar to the formula for an annuity, the present value of a growing annuity (PVGA) uses the same variables with the addition of g as the rate of growth of the annuity (A is the annuity payment in the first period). This is a calculation that is rarely provided for on financial calculators.
Where i ≠ g :
Where i = g :
To get the PV of a growing annuity due, multiply the above equation by (1 + i).
Present value of a perpetuity
A perpetuity is payments of a set amount of money that occur on a routine basis and continues forever. When n → ∞, the PVof a perpetuity (a perpetual annuity) formula becomes simple division.
Present Value of Int Factor Annuity
Example:
- Investment P = $1000
- Interest i = 6.90% Compounded Qtrly (4 Times in Year)
- Tenure Years n = 5

Present value of a growing perpetuity
When the perpetual annuity payment grows at a fixed rate (g) the value is theoretically determined according to the following formula. In practice, there are few securities with precise characteristics, and the application of this valuation approach is subject to various qualifications and modifications. Most importantly, it is rare to find a growing perpetual annuity with fixed rates of growth and true perpetual cash flow generation. Despite these qualifications, the general approach may be used in valuations of real estate, equities, and other assets.
This is the well known Gordon Growth model used for stock valuation.
Future value of an annuity
The future value of an annuity (FVA) formula has four variables, each of which can be solved for:
To get the FV of an annuity due, multiply the above equation by (1 + i).
Future value of a growing annuity
The future value of a growing annuity (FVA) formula has five variables, each of which can be solved for:
Where i ≠ g :
Where i = g :



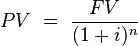
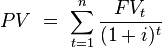
![PV(A) \,=\,\frac{A}{i} \cdot \left[ {1-\frac{1}{\left(1+i\right)^n}} \right]](https://upload.wikimedia.org/math/c/b/6/cb63bc7899b0197bc65963ea0fe6e2f3.png)
![PV\,=\,{A \over (i-g)}\left[ 1- \left({1+g \over 1+i}\right)^n \right]](https://upload.wikimedia.org/math/2/9/d/29def358b418103f96d8e8b50e016cfa.png)
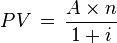


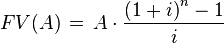



No comments:
Post a Comment